题目内容
13.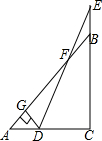 如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是线段AC上的点,点E是线段CB延长线上的点,且BE=AD,连接DE交AB于点F,过点D作DG⊥AB,垂足为G,则线段FG的长为$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是线段AC上的点,点E是线段CB延长线上的点,且BE=AD,连接DE交AB于点F,过点D作DG⊥AB,垂足为G,则线段FG的长为$\sqrt{2}$.
分析 过D点作DH∥BC交AB于点H,由DH∥BC得到∠ADH=90°,又因为∠A=45°,所以AD=DH,证明△DHF≌△EBF,得到HF=BF,所以DG=GH+FH=$\frac{1}{2}$AB,即可求解.
解答 解:过D点作DH∥BC交AB于点H,
∴∠HDE=∠BEF,
∵∠ACB=90°,AC=BC,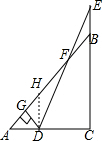
∴∠ADH=90°,∠A=45°,
∴AD=DH,
∵BE=AD,
∴DH=EB
在△DHF和△EBF中,
$\left\{\begin{array}{l}{∠HDE=∠BEF}\\{∠HFD=∠BFE}\\{DH=EB}\end{array}\right.$,
∴△DHF≌△EBF,
∴HF=BF,
∴FG=GH+FH=$\frac{1}{2}$AB,
∵∠ACB=90°,AC=BC=2,
∴AB=2$\sqrt{2}$,
∴FG=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了全等三角形的判定与性质以及等腰直角三角形的性质,作出辅助线构造三角形全等是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
8.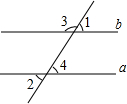 如图,不能确定直线a∥b的条件是( )
如图,不能确定直线a∥b的条件是( )
 如图,不能确定直线a∥b的条件是( )
如图,不能确定直线a∥b的条件是( )| A. | ∠1=∠2 | B. | ∠3+∠4=180° | C. | ∠2+∠3=180° | D. | ∠1+∠3=180° |
 如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.
如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA. 如图,四边形ABCD的四个顶点的坐标分别为A(-2,2),B(-4,-3),C(3,-3),D(2,1),求四边形ABCD的面积.
如图,四边形ABCD的四个顶点的坐标分别为A(-2,2),B(-4,-3),C(3,-3),D(2,1),求四边形ABCD的面积.