题目内容
9.直线y=-2x+4与x轴交于点A,与y轴交于点B,直线y=kx+b(k,b是常数,k≠0)经过点A,与y轴交于点C,且OC=OA.(1)求点A的坐标及k的值;
(2)点C在x轴的上方,点P在直线y=-2x+4上,若PC=PB,求点P的坐标.
分析 (1)令y=0,求得x的值,即可求得A的坐标为(2,0),由OC=OA得C(0,2)或(0,-2),然后根据待定系数法即可求得k的值;
(2)由B、C的坐标,根据题意求得P的纵坐标,代入y=-2x+4即可求得横坐标.
解答 解:(1)由直线y=-2x+4与x轴交于点A,与y轴交于点B,
令y=0,则-2x+4=0,
解得x=2,
∴A(2,0),
∵OC=OA,
∴C(0,2)或(0,-2),
∵直线y=kx+b(k,b是常数,k≠0)经过点A和点C,
∴$\left\{\begin{array}{l}{2k+b=0}\\{b=-2}\end{array}\right.$或$\left\{\begin{array}{l}{2k+b=0}\\{b=2}\end{array}\right.$,
解得k=1或k=-1;
(2)∵B(0,4),C(0,2),且PC=PB,
∴P的纵坐标为3,
∵点P在直线y=-2x+4上,
把y=3代入y=-2x+4解得x=$\frac{1}{2}$,
∴P($\frac{1}{2}$,3).
点评 本题考查了一次函数图象上点点坐标特征,分类讨论思想运用是本题点关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
4.对于反比例函数y=$\frac{6}{x}$,当1<x<2时,y的取值范围是( )
| A. | 1<y<3 | B. | 2<y<3 | C. | 1<y<6 | D. | 3<y<6 |
14.初三(1)班体育委员统计本班30名同学体育中考成绩数据如下表所示:
则这30名同学成绩的众数和中位数分别是( )
| 成绩 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数 | 2 | 3 | 5 | 6 | 10 | 4 |
| A. | 29,30 | B. | 29,28 | C. | 28,30 | D. | 28,28 |

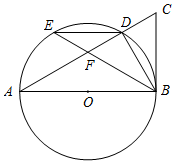 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.