题目内容
18.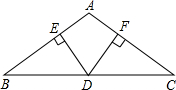 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.(1)若BD=DC,求证:DE=DF;
(2)若∠BAC=120°,DE+DF=5,求BC的长.
分析 (1)根据AAS证明△BDE≌△CDF即可得证;
(2)先根据等腰三角形的性质及三角形内角和定理求出∠B=∠C=30°,根据直角三角形30°角所对的直角边等于斜边的一半得到DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,两式相加,可知DE+DF=$\frac{1}{2}$BC,即可求出BC的长.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{∠BED=∠CFD=90°}\\{∠B=∠C}\\{BD=DC}\end{array}\right.$,
∴△BDE≌△CDF,
∴DE=DF;
(2)解∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,
∴DE+DF=$\frac{1}{2}$BD+$\frac{1}{2}$DC=$\frac{1}{2}$(BD+DC)=$\frac{1}{2}$BC.
∵DE+DF=5,
∴BC=10.
点评 此题主要考查了全等三角形的判定与性质、等腰三角形的性质、三角形内角和定理及含30度角的直角三角形的性质的综合运用,熟练地综合运用几何知识是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的常数项为0,则m的值是______.
的常数项为0,则m的值是______.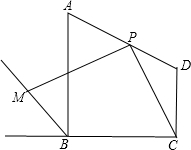 已知:梯形ABCD中,AB∥CD,P是AD中点,M是梯形ABCD外角∠ABE的平分线上一点,且∠CPM=90°,如图,当∠ABC=90°时,探究PC与PM之间的数量关系.
已知:梯形ABCD中,AB∥CD,P是AD中点,M是梯形ABCD外角∠ABE的平分线上一点,且∠CPM=90°,如图,当∠ABC=90°时,探究PC与PM之间的数量关系.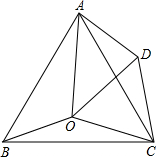 如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.
如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.
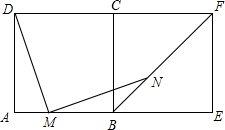 如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.
如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.