题目内容
20.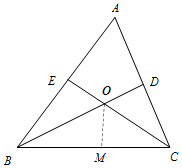 如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.
如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.(1)∠BOC=120°;
(2)将△ABC沿BD所在直线折叠,若点E落在BC上的M处,试证明:CM=CD.
分析 (1)先根据三角形内角和得:∠ACB+∠ABC=120°,由角平分线定义得:∠OBC+∠OCB=60°,最后由三角形内角和可得结论;
(2)证明△DCO≌△MCO可得结论.
解答 解:(1)∵∠A=60°,
∴∠ACB+∠ABC=180°-60°=120°,
∵∠ABC的平分线BD与∠ACB的平分线CE相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$×120°=60°,
∴∠BOC=180°-60°=120°,
故答案为:120;
(2)连接OM,
∵∠BOC=120°,
∴∠BOE=60°,
由翻叠的性质可得:△BOE≌△BOM,
∴∠BOE=∠BOM=60°,
∴∠MOC=∠DOC=60°,
∵OC为∠DCM的角平分线,
∴∠DCO=∠MCO,
在△DCO与△MCO中,
∵$\left\{\begin{array}{l}{∠DCO=∠MCO}\\{OC=OC}\\{∠MOC=∠DOC}\end{array}\right.$,
∴△DCO≌△MCO (ASA),
∴CM=CD.
点评 本题考查了角平分线的定义、三角形内角和定理、三角形全等的性质和判定、翻折的性质,熟练掌握翻折的性质是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | (a2)3=a6 | C. | 2x+3y=5xy | D. | 2-3=-6 |
15.一家游泳馆的游泳收费标准为25元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员卡,一年内游泳20次,消费50+20×20=450元,若一年内在该游泳馆消费500元,则游泳次数最多的办卡方式是( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 50 | 20 |
| B类 | 150 | 15 |
| C类 | 300 | 10 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
12.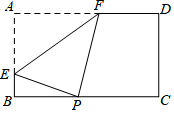 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )| A. | $\sqrt{5}≤BP≤5$ | B. | 2≤BP≤6 | C. | $\sqrt{5}≤BP≤6$ | D. | $2≤BP≤5\sqrt{3}$ |
 如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.