题目内容
11. 如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.
分析 连接AC交BD于O,连接PC,作CQ′⊥AD于Q′交BD于P′.根据S菱形ABCD=$\frac{1}{2}$•BD•AC=AD•CQ′,可以求出CQ′,由BD垂直平分AC,推出PA=PC,推出PA+PQ=PC+PQ,推出当P与P′重合,Q与Q′重合时,PA+PQ的值最小.
解答 解:连接AC交BD于O,连接PC,作CQ′⊥AD于Q′交BD于P′.
∵四边形ABCD是菱形,
∴BD⊥AC,OB=OD=4,
∵AB=5,
∴OA=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AC=6,
∴S菱形ABCD=$\frac{1}{2}$•BD•AC=AD•CQ′,
∴CQ′=$\frac{24}{5}$,
∵BD垂直平分AC,
∴PA=PC,
∴PA+PQ=PC+PQ,
∴当P与P′重合,Q与Q′重合时,PA+PQ的值最小,最小值为CQ′=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查菱形的性质、轴对称最短问题、垂线段最短、勾股定理等知识,解题的关键是学会利用对称解决最值问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
6. 如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
 如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )| A. | 75° | B. | 30° | C. | 45° | D. | 105° |
 如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4.
如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4. 已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.
已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.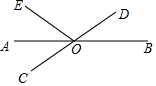 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.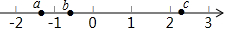 已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.
已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.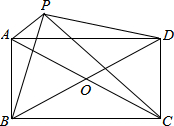 如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.
如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.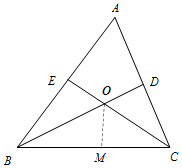 如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.
如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O. 如图所示,在△ABC中,∠B=60°,BC=2,中线CD⊥BC,求AC,sinA的值.
如图所示,在△ABC中,∠B=60°,BC=2,中线CD⊥BC,求AC,sinA的值.