题目内容
12.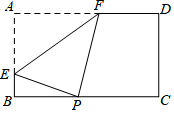 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )| A. | $\sqrt{5}≤BP≤5$ | B. | 2≤BP≤6 | C. | $\sqrt{5}≤BP≤6$ | D. | $2≤BP≤5\sqrt{3}$ |
分析 要使折痕始终与边AB,AD有交点,就要找到F与D重合,E与B重合时对应BP的长即可,由折叠可得结论.
解答  解:当F与D重合时,如图1,
解:当F与D重合时,如图1,
由折叠得:AD=AP=10,
∵四边形ABCD是矩形,
∴∠C=90°,
∵AB=DC=6,
在Rt△PDC中,PC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴BP=10-8=2;
当E与B重合时,如图2,
由折叠得:AB=BP=6,
综上所述,BP的取值范围是:2≤BP≤6;
故选B.
点评 本题考查了矩形的性质、折叠的性质、勾股定理,注意利用数形结合的思想,与折叠的性质相结合,使问题得以解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.
已知如图,∠ABC=60°,BM平分∠ABC,过BM上任意一点D(D点不与B点重合)作BC的平行线交AB于点E.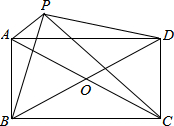 如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.
如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.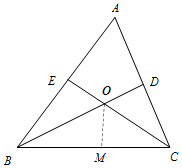 如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.
如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.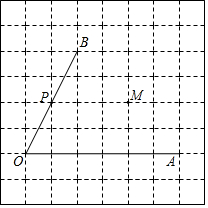 如图,点P是∠AOB的边OB上的一点.
如图,点P是∠AOB的边OB上的一点.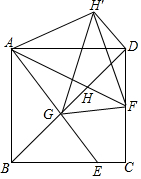 如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4.
如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4. 如图所示,在△ABC中,∠B=60°,BC=2,中线CD⊥BC,求AC,sinA的值.
如图所示,在△ABC中,∠B=60°,BC=2,中线CD⊥BC,求AC,sinA的值.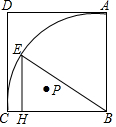 如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.
如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.