题目内容
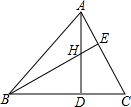 如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.
如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.考点:全等三角形的判定与性质
专题:
分析:根据同角的余角相等求出∠CAD=∠HBD,再利用“角角边”证明△ACD和△BHD全等,根据全等三角形对应边相等可得AD=BD,然后判断出△ABD是等腰直角三角形,根据等腰直角三角形的性质解答即可.
解答:解:∵AD、BE是△ABC的高,
∴∠CAD+∠C=∠HBD+∠C,
∴∠CAD=∠HBD,
在△ACD和△BHD中,
,
∴△ACD≌△BHD(AAS),
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABC=45°.
∴∠CAD+∠C=∠HBD+∠C,
∴∠CAD=∠HBD,
在△ACD和△BHD中,
|
∴△ACD≌△BHD(AAS),
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABC=45°.
点评:本题考查了全等三角形的判定与性质,同角的余角相等的性质,等腰直角三角形的判定与性质,熟记性质并求出三角形全等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )
如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )| A、45° | B、55° |
| C、60° | D、75° |
下列说法中,正确的是( )
| A、无理数都是无限小数 | ||
| B、带根号的数都是无理数 | ||
C、
| ||
| D、9的平方根是3 |
下列命题中,逆命题正确的是( )
| A、全等三角形的对应角相等 |
| B、全等三角形的周长相等 |
| C、全等三角形的面积相等 |
| D、全等三角形的对应边相等 |
 如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.
如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.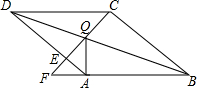 在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.