题目内容
9．
如图，D为△ABC内的一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为24．
分析 由四边形DEBF为矩形得到DE=BF=9，DF∥BE，∠DFB=∠DEB=90°，推出△CDF∽△DGE，得到$\frac{CD}{DG}=\frac{CF}{DE}=\frac{2}{3}$，由于S△ADG=$\frac{1}{2}$AG•DE=$\frac{1}{2}×8×9$=36，于是得到S△ADC=$\frac{2}{3}$S△ADG=24，
解答 解：∵四边形DEBF为矩形，
∴DE=BF=9，DF∥BE，∠DFB=∠DEB=90°，
∴∠DEG=∠DFC=90°，∠CDF=∠DGE，
∴△CDF∽△DGE，
∴$\frac{CD}{DG}=\frac{CF}{DE}=\frac{2}{3}$，
∵S△ADG=$\frac{1}{2}$AG•DE=$\frac{1}{2}×8×9$=36，
∴S△ADC=$\frac{2}{3}$S△ADG=24，
故答案为：24．
点评 本题考查了三角形的面积，矩形的性质，本题关键是活用三角形面积公式进行计算．
练习册系列答案
相关题目
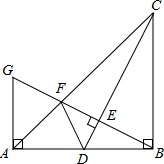如图，在Rt△ABC中，∠ABC=90°，BA=BC，点D是AB的中点，连接CD，过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G．