题目内容
3.已知:$\sqrt{a}$-$\frac{1}{\sqrt{a}}$=2$\sqrt{3}$,求$\sqrt{a}$+$\frac{1}{\sqrt{a}}$的值.分析 根据($\sqrt{a}$+$\frac{1}{\sqrt{a}}$)2=($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2+4代入即可计算,注意$\sqrt{a}$+$\frac{1}{\sqrt{a}}$>0这个隐含条件.
解答 解:∵($\sqrt{a}$+$\frac{1}{\sqrt{a}}$)2=($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2+4=(2$\sqrt{3}$)2+4=16,
∵$\sqrt{a}$+$\frac{1}{\sqrt{a}}$>0,
∴$\sqrt{a}$+$\frac{1}{\sqrt{a}}$=4.
点评 本题考查二次根式化简求值,乘法公式,解题的关键是掌握公式变形,记住($\sqrt{a}$+$\frac{1}{\sqrt{a}}$)2=($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2+4,注意$\sqrt{a}$+$\frac{1}{\sqrt{a}}$>0这个隐含条件,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.数学老师说了下面四句话,其中可以作为定理使用的是( )
| A. | 同位角相等 | B. | 两点之间线段最短 | ||
| C. | 同旁内角互补 | D. | 对顶角相等 |
 在平面直角坐标系xOy中,直线y=$\frac{3}{4}$x+1与x轴交于点A,且与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B($\frac{8}{3}$,m).
在平面直角坐标系xOy中,直线y=$\frac{3}{4}$x+1与x轴交于点A,且与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B($\frac{8}{3}$,m). 如图,若∠B=50°,则∠∠ADE=50°时,DE∥BC,理由是同位角相等,两直线平行.
如图,若∠B=50°,则∠∠ADE=50°时,DE∥BC,理由是同位角相等,两直线平行.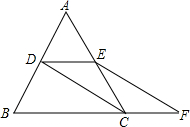 如图,等边三角形ABC的边长是2,D、E分别为AB、AC的中点,点F在BC延长线上,且CF=$\frac{1}{2}BC$,求四边形DEFB的面积.
如图,等边三角形ABC的边长是2,D、E分别为AB、AC的中点,点F在BC延长线上,且CF=$\frac{1}{2}BC$,求四边形DEFB的面积.