Question

13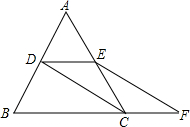．如图，等边三角形ABC的边长是2，D、E分别为AB、AC的中点，点F在BC延长线上，且CF=$\frac{1}{2}BC$，求四边形DEFB的面积．

Answer 1

分析 由三角形的中位线定理得到DE=CF，DE∥CF，证得四边形DEFC是平行四边形，即可证得S_△ECF=S_△DEC=S_△ADE，即可证得S_{四边形DEFB}=S_△ABC，求得△ABC的面积即可．

解答 解：∵点D、E分别是AB、AC的中点，
∴DE=$\frac{1}{2}$BC，DE∥BF，
∵CF=$\frac{1}{2}BC$，
∴DE=CF，DE∥CF，
∴四边形DEFC是平行四边形，
∴S_△ECF=S_△DEC=S_△ADE，
∵△ABC是等边三角形，D是AB的中点，
∴CD⊥AB，AD=BD=1，BC=2，
∴DC=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{3}$
∴S_{四边形DEFB}=S_△ABC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$．

点评 本题考查了三角形中位线定理，平行四边形的判定和性质，勾股定理的应用，证得S_△ECF=S_△DEC=S_△ADE是本题的关键．