题目内容
11.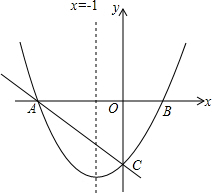 如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.
如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.(1)求抛物线的解析式.
(2)点C为抛物线与y轴的交点.
①点P在抛物线上,且S△POC=4S△BOC,求点P点坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
分析 (1)因为抛物线的对称轴为x=-1,A点坐标为(-3,0)与(2,5)在抛物线上,代入抛物线的解析式,即可解答;
(2)①先由二次函数的解析式为y=x2+2x-3,得到C点坐标,然后设P点坐标为(x,x2+2x-3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②先运用待定系数法求出直线AC的解析式为y=-x-3,再设Q点坐标为(x,-x-3),则D点坐标为(x,x2+2x-3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
解答 解:(1)因为抛物线的对称轴为x=-1,A点坐标为(-3,0)与(2,5)在抛物线上,则:
$\left\{\begin{array}{l}{9a-3b+c=0}\\{4a+2b+c=5}\\{-\frac{b}{2a}=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\\{c=-3}\end{array}\right.$.
所以抛物线的解析式为:y=x2+2x-3.
(2)二次函数的解析式为y=x2+2x-3,
∴抛物线与y轴的交点C的坐标为(0,-3),OC=3.
设P点坐标为(x,x2+2x-3),
∵S△POC=4S△BOC,
∴$\frac{1}{2}$×3×|x|=4×$\frac{1}{2}$×3×1,
∴|x|=4,x=±4.当x=4时,x2+2x-3=16+8-3=21;
当x=-4时,x2+2x-3=16-8-3=5.
∴点P的坐标为(4,21)或(-4,5);
(3)设直线AC的解析式为y=kx+t,将A(-3,0),C(0,-3)代入,
得$\left\{\begin{array}{l}{-3k+t=0}\\{t=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{t=-3}\end{array}\right.$.
即直线AC的解析式为y=-x-3.
设Q点坐标为(x,-x-3)(-3≤x≤0),则D点坐标为(x,x2+2x-3),
QD=(-x-3)-(x2+2x-3)=-x2-3x=-$(x+\frac{3}{2})^{2}+\frac{9}{4}$,
∴当x=-$\frac{3}{2}$时,QD有最大值$\frac{9}{4}$.
点评 此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案| A. | (-2,3) | B. | (0,-2) | C. | (-4,4) | D. | (-4,-2) |
①平分弦的直径垂直于弦;
②三角形的三个顶点确定一个圆;
③圆内接四边形的对角相等;
④圆的切线垂直于过切点的半径;
⑤过圆外一点所画的圆的两条切线长相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
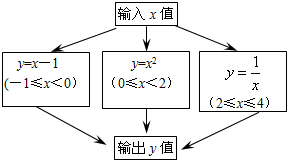
| A. | $\frac{2}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{25}$ | D. | $\frac{25}{4}$ |
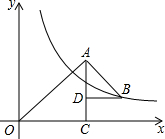 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )