题目内容
16.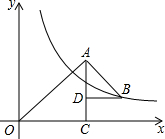 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
分析 根据题意得到OA=$\sqrt{2}$OC,AB=$\sqrt{2}$BD,由已知得OC2-DB2=6,因为点B的横坐标为:OC+BD,纵坐标为OC-BD,求出k的值.
解答 解:由题意可知,OC=AC,DB=DA,OA=$\sqrt{2}$OC,AB=$\sqrt{2}$BD,
点B的横坐标为:OC+BD,纵坐标为OC-BD,
∵OA2-AB2=12,∴OC2-DB2=6,即(OC+BD)(OC-BD)=6,
∴k=6,
故选:B.
点评 本题考查的是等腰三角形的性质和待定系数法求反比例函数的解析式,正确表示出点B的坐标是解题的关键,解答时,注意因式分解的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
 如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
如图,如果点M的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
1.若实数x、y满足x2=$\sqrt{\frac{1}{2}y-\frac{1}{2}}$+$\sqrt{3-3y}$+4,则x+y的值是( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
5.把分式$\frac{x+y}{x-3y}$中的x和y都扩大为原来的2倍,则分式的值( )
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |
6.已知a=-(0.2)2,b=-2-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a、b、c、d的大小关系是( )
| A. | a<b<d<c | B. | b<a<d<c | C. | a<b<c<d | D. | b<a<c<d |
 如图,有足够多的长方形和正方形卡片,
如图,有足够多的长方形和正方形卡片,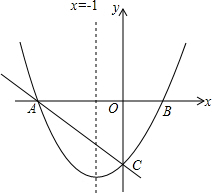 如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.
如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.