题目内容
1.计算:(1)2$\sqrt{2}$-|$\sqrt{2}$-$\sqrt{3}$|
(2)$\sqrt{4}$+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$.
分析 (1)原式利用绝对值的代数意义化简,合并即可得到结果;
(2)原式利用平方根及立方根定义计算即可得到结果.
解答 解:(1)原式=2$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$=3$\sqrt{2}$-$\sqrt{3}$;
(2)原式=2-2-$\frac{1}{2}$=-$\frac{1}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列二次根式中能与$\sqrt{2}$合并的二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
6.已知a=-(0.2)2,b=-2-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a、b、c、d的大小关系是( )
| A. | a<b<d<c | B. | b<a<d<c | C. | a<b<c<d | D. | b<a<c<d |
10.-2的相反数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
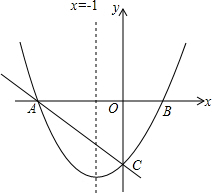 如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.
如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.
 如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.
如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.