题目内容
7.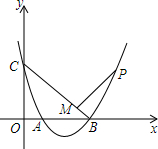 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
分析 要求点P的坐标,只要设出点P的坐标,根据点P在抛物线上,由抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,可以得到点P的横纵坐标之间的关系,从而可以求得点P的坐标.
解答 解:将y=0代入y=x2-3x+2得x=1或x=2,将x=0代入y=x2-3x+2得,y=2,
∵抛物线y=x2-3x+2与坐标轴交于A、B、C三点,
∴点A(1,0),点B(2,0),点C(0,2),
∴OC=OB,
∴∠OCB=∠OBC=90°,
作PN⊥y轴于点N交BC于点D,如右图所示,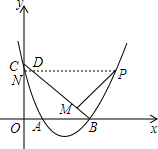 ∴△CND和△PMD是等腰直角三角形,
∴△CND和△PMD是等腰直角三角形,
设PM=a,则MD=a,CM=2a,
∴CD=a,
∴ND=CD•sin45°=$\frac{\sqrt{2}a}{2}$,PD=$\frac{a}{sin45°}=\sqrt{2}a$,
∴点P的坐标为($\frac{\sqrt{2}a}{2}+\sqrt{2}a$,2-$\frac{\sqrt{2}a}{2}$),
即点P的坐标为($\frac{3\sqrt{2}a}{2},2-\frac{\sqrt{2}a}{2}$)
∵点P在抛物线上,
∴$(\frac{3\sqrt{2}a}{2})^{2}-3×\frac{3\sqrt{2}a}{2}+2=2-\frac{\sqrt{2}a}{2}$,
解得,a=$\frac{8\sqrt{2}}{9}$或a=0(舍去),
∴点P的坐标为($\frac{8}{3},\frac{10}{9}$).
点评 本题考查抛物线与x轴的交点,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
相关题目
8.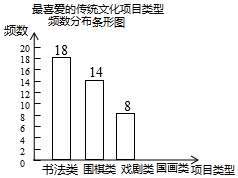 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.最喜爱的传统文化项目类型频数分布表
| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
9. 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
如图是一个正方体纸盒的外表面展开图,则这个正方体是( )| A. |  | B. |  | C. |  | D. |  |
6.下列计算正确的是( )
| A. | $\frac{x^2}{y^2}=\frac{x}{y}(y≠0)$ | B. | xy2÷$\frac{1}{2y}=2xy({y≠0})$ | ||
| C. | 2$\sqrt{x}+3\sqrt{y}=5\sqrt{xy}({x≥0,y≥0})$ | D. | (xy3)2=x2y6 |
 在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.
在⊙O中,弦AB=3,将AB绕点O逆时针旋转60°得弦A′B′,连接OA′,已知OA′⊥AB于C,求⊙O的半径.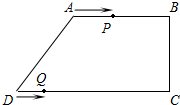 如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).
如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).