题目内容
17.先化简,再求值:$\frac{{{x^2}-6x+9}}{2x-6}$•(x+3),其中x-$\sqrt{3}$=0.分析 根据分式的乘法法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{{(x-3)}^{2}}{2(x-3)}$•(x+3)
=$\frac{{{x^2}-9}}{2}$.
∵x-$\sqrt{3}$=0,
∴x=$\sqrt{3}$,
∴原式=$\frac{{(\sqrt{3})}^{2}-9}{2}$=-3.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |
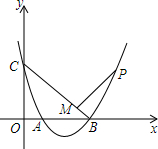 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标. 三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.
三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.
 如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$).
如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$). 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: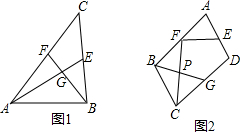
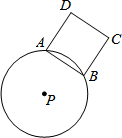 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.