题目内容
12.若正比例函数y=(1-4m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时y1>y2,则m的最小整数解是1.分析 根据A、B两点坐标的特点,可以得知该正比例函数y值随x的增大而减小,即k=1-4m<0,解不等式得出m的取值范围,再取其内的最小整数即可得出结论.
解答 解:∵点A(x1,y1)和点B(x2,y2)在正比例函数图象上,且当x1<x2时y1>y2,
∴该正比例函数y值随x的增大而减小,
∴1-4m<0,解得:m>$\frac{1}{4}$.
∴m的最小整数解是1.
故答案为:1.
点评 本题考查了一次函数图象上点的坐标特征以及一次函数的性质,解题的关键是找出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的单调性确定k的正负是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
17.计算(-3)×4的结果是( )
| A. | 12 | B. | -12 | C. | -1 | D. | -7 |
4.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数,设个位数字为x,十位数字为y,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |
2.下列说法正确的是( )
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |



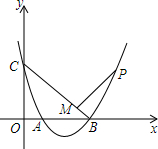 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标. 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题: