题目内容
19.先化简,再求值:$\frac{{a}^{3}b+{a}^{2}{b}^{2}}{{a}^{2}+2ab+{b}^{2}}$÷$\frac{{a}^{2}-ab}{{a}^{2}-{b}^{2}}$,其中a=2-$\sqrt{2}$,b=2+$\sqrt{2}$.分析 先根据分式的除法法则把原式进行化简,再把a、b的值代入进行计算即可.
解答 解:原式=$\frac{{a}^{2}b(a+b)}{(a+b)^{2}}$•$\frac{(a+b)(a-b)}{a(a-b)}$
=$\frac{{a}^{2}b}{a+b}$•$\frac{a+b}{a}$
=ab,
当a=2-$\sqrt{2}$,b=2+$\sqrt{2}$时,原式=(2-$\sqrt{2}$)(2+$\sqrt{2}$)=4-2=2.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意把分式化为最简形式,再代入求值.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.计算:($\frac{21}{26}$)3×($\frac{13}{14}$)4×($\frac{4}{3}$)5=( )
| A. | $\frac{13}{33}$ | B. | $\frac{104}{63}$ | C. | $\frac{2×13}{3×7}$ | D. | $\frac{23×13}{32×7}$ |
4.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数,设个位数字为x,十位数字为y,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |

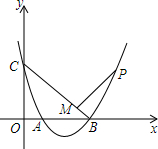 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标. 三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.
三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: