题目内容
解方程组:
.
|
考点:解三元一次方程组
专题:
分析:观察所给方程组的结构特点,运用加减消元法,首先消去字母z,将三元方程组转化为二元方程组;解二元方程组即可解决问题.
解答:解:
由①+②得:3x+4y=10④,
由②+③得:5x+2y=12⑤;
由④-2×⑤得:-7x=-14,
∴x=2,代入④并解得:y=1,
将x=2,y=1代入①并解得:z=3,
∴原方程组的解为:
.
|
由①+②得:3x+4y=10④,
由②+③得:5x+2y=12⑤;
由④-2×⑤得:-7x=-14,
∴x=2,代入④并解得:y=1,
将x=2,y=1代入①并解得:z=3,
∴原方程组的解为:
|
点评:该题主要考查了三元一次方程组的解法问题;解题的关键是深入把握所给方程组的结构特点,灵活选用代入法或加减消元来分析、判断、推理或解答;对求解运算能力提出了较高的要求.

练习册系列答案
相关题目
 如图,?ABCD中AC,BD是对角线,AC∥DE,AE∥BD,连接DE,BE,那么图中和△ABC面积相等的三角形共有
如图,?ABCD中AC,BD是对角线,AC∥DE,AE∥BD,连接DE,BE,那么图中和△ABC面积相等的三角形共有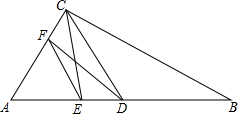 如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE=
如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE= 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,AD与EF交于点G,请探索EF与AD的关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,AD与EF交于点G,请探索EF与AD的关系,并说明理由.