题目内容
如果|m-1|+(n+2)2=0,那么(m+n)2005= .
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:根据非负数的性质可求出m、n的值,再将它们代入(m+n)2005中求解即可.
解答:解:∵m、n满足|m-1|+(n+2)2=0,
∴m-1=0,m=1;
n+2=0,n=-2;
则(m+n)2005=(-1)2005=-1.
故答案为:-1.
∴m-1=0,m=1;
n+2=0,n=-2;
则(m+n)2005=(-1)2005=-1.
故答案为:-1.
点评:本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,?ABCD中AC,BD是对角线,AC∥DE,AE∥BD,连接DE,BE,那么图中和△ABC面积相等的三角形共有
如图,?ABCD中AC,BD是对角线,AC∥DE,AE∥BD,连接DE,BE,那么图中和△ABC面积相等的三角形共有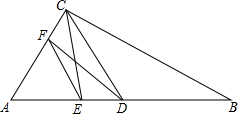 如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE=
如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE=