题目内容
12.-$\frac{{x{y^2}}}{7}$的系数为-$\frac{1}{7}$.分析 将单项式进行变形,变形后即可找出单项式的系数.
解答 解:∵-$\frac{x{y}^{2}}{7}$=-$\frac{1}{7}$xy2,
∴-$\frac{{x{y^2}}}{7}$的系数为-$\frac{1}{7}$.
故答案为:-$\frac{1}{7}$.
点评 本题考查了单项式,能够熟练找出单项式的次数与系数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的是( )
①抛物线与x轴的一个交点为(3,0);
②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是直线x=$\frac{1}{2}$;
④在对称轴左侧,y随x增大而增大.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0);
②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是直线x=$\frac{1}{2}$;
④在对称轴左侧,y随x增大而增大.
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
20.盒中原有8个小球,一位魔术师从中任意取几个小球,把每一个小球都变成了8个小球,将其放回盒中,他又从盒中任取一些小球,把每一个小球又都变成了8个小球后放回盒中,如此进行到某一时刻魔术师停止取球变球时,盒中球的总数可能是( )
| A. | 2010个 | B. | 2011个 | C. | 2012个 | D. | 2013个 |
2.满足等式(x+3)${\;}^{-{x}^{2}+x+2}$=1的所有实数x的和是( )
| A. | 1 | B. | -1 | C. | -5 | D. | -6 |
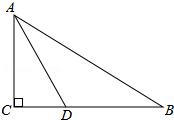 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是2$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是2$\sqrt{3}$.