题目内容
 如图,?ABCD中,对角线AC、BD相交于点O,AF⊥BD、CE⊥BD,垂足分别为F、E,连结AE、CF,试判断四边形AFCE的形状并证明你的结论.
如图,?ABCD中,对角线AC、BD相交于点O,AF⊥BD、CE⊥BD,垂足分别为F、E,连结AE、CF,试判断四边形AFCE的形状并证明你的结论.考点:平行四边形的判定与性质
专题:
分析:四边形AFCE为平行四边形;可先证明△AOF≌△COE,可得OF=OE,又有OA=OC,根据对角线互相平分的四边形是平行四边形,可得四边形AFCE是平行四边形.
解答:解: 四边形AFCE是平行四边形.理由如下:
四边形AFCE是平行四边形.理由如下:
∵AF⊥BD、CE⊥BD,
∴∠AFO=∠CEO=90°.
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴OF=OE.
又∵OA=OC,
∴四边形AFCE是平行四边形.
 四边形AFCE是平行四边形.理由如下:
四边形AFCE是平行四边形.理由如下:∵AF⊥BD、CE⊥BD,
∴∠AFO=∠CEO=90°.
在△AOF和△COE中,
|
∴△AOF≌△COE(AAS),
∴OF=OE.
又∵OA=OC,
∴四边形AFCE是平行四边形.
点评:本题考查了平行四边形的性质和判定,其中平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
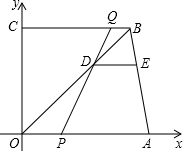 如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s) 如图,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,直线OQ与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
如图,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,直线OQ与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.