题目内容
5.化简($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$,并解答:(1)已知|$\sqrt{2}$-x|=0,求原代数式的值;
(2)原代数式的值能等于-2吗?为什么?
分析 (1)根据|$\sqrt{2}$-x|=0得出x=$\sqrt{2}$,再代入化简后的分式即可;
(2)设化简后的分式的值等于-2,利用分式的有意义的条件解答即可.
解答 解:(1)($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$
=$[\frac{2x(x+1)}{(x+1)(x-1)}-\frac{x(x-1)}{(x-1)^{2}}]×\frac{x+1}{x}$
=$(\frac{2x}{x-1}-\frac{x}{x-1})×\frac{x+1}{x}$
=$\frac{x}{x-1}×\frac{x+1}{x}$
=$\frac{x+1}{x-1}$,
∵|$\sqrt{2}$-x|=0,
∴$\sqrt{2}-x=0$,
得,x=$\sqrt{2}$,
当x=$\sqrt{2}$时,原式=$\frac{x+1}{x-1}=\frac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}$;
(2)原代数式的值能等于-2.
理由:当$\frac{x+1}{x-1}=-2$时,
解得,x=$\frac{1}{3}$,
检验:当x=$\frac{1}{3}$时,原分式有意义,
所以原代数式的值能等于-2.
点评 本题考查分式的化简求值,解题的关键是在化简中一定要仔细认真,注意解得的分式方程的解还要检验是否使得原分式方程有意义.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
15.下列计算正确的是( )
| A. | (x+y)(y-x)=x2-y2 | B. | (-x+2y)2=x2-4xy+4y2 | ||
| C. | (2x-$\frac{1}{2}$y)2=4x2-xy+$\frac{1}{4}$y2 | D. | (-3x-2y)2=9x2-12xy+4y2 |
10.在直角三角形ABC中,∠C=90°,AC=3,BC=4 若以C为圆心,以2.5为半径做圆C,则圆C与AB所在直线的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
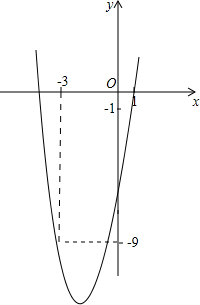 如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9). 如图,四边形ABCD内接于⊙O,AB是直径,∠ABD=30°,则∠BCD的度数为多少?
如图,四边形ABCD内接于⊙O,AB是直径,∠ABD=30°,则∠BCD的度数为多少?