题目内容

5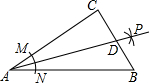．如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（　　）
A．30B．45C．60D．90

分析 作DE⊥AB于E，根据角平分线的性质得到DE=DC=6，根据三角形的面积公式计算即可．

解答 解：作DE⊥AB于E，
由基本作图可知，AP平分∠CAB，
∵AP平分∠CAB，∠C=90°，DE⊥AB，
∴DE=DC=6，
∴△ABD的面积=$\frac{1}{2}$×AB×DE=60，
故选：C．

点评 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．

练习册系列答案
相关题目
15．25的平方根是（　　）
A．5B．-5C．±5D．±$\sqrt{5}$
16．下列各组的两个单项式中，属于同类项的是（　　）
A．3m2n2与-m2n3B．$\frac{2}{3}$xy与2yx2
C．53与a3D．-32x2y2与-23x2y2
13．将抛物线y=2x2先向上平移2个单位，再向右平移3个单位，则所得解析式是（　　）
A．y=2（x-3）2+2B．y=2（x-3）2-2C．y=2（x+3）2-2D．y=2（x+3）2+2
20．下列各点中，抛物线y=x2-4x-4经过的点是（　　）
A．（0，4）B．（1，-7）C．（-1，-1）D．（2，8）
10．抛物线y=x2-bx+9的顶点在坐标轴上，则b的值为（　　）
A．6B．±6C．±6或0D．0
17．下列分式中不是最简分式的是（　　）
A．$\frac{3x}{4x+3}$B．$\frac{x-y}{x{y}^{2}-{x}^{2}y}$C．$\frac{2y}{3x}$D．$\frac{x+{y}^{2}}{x{y}^{3}-{x}^{2}y}$
14．下列方程是一元二次方程的是（　　）
A．x2-1=yB．（x+2）（x+1）=x2C．6x2=5D．x+1=$\frac{1}{x}$
15．一种细菌的半径约为0.00004米，这个数用科学记数法表示为（　　）
A．4×10-5B．0.4×10-6C．4×10-4D．40×10-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网