题目内容
20．下列各点中，抛物线y=x2-4x-4经过的点是（ ）| A． | （0，4） | B． | （1，-7） | C． | （-1，-1） | D． | （2，8） |
分析 分别计算出自变量为0、1、-1、和2所对应的函数值，然后根据二次函数图象上点的坐标特征进行判断．
解答 解：当x=0时，y=x2-4x-4=-4；当x=1时，y=x2-4x-4=-7；当x=-1时，y=x2-4x-4=1；当x=2时，y=x2-4x-4=-8，
所以点（1，-7）在抛物线y=x2-4x-4上．
故选B．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
名校课堂系列答案
相关题目
10．红光机械厂九月份生产零件50万个，十一月份生产零件72万个，设该机械厂九、十月份生产零件数量的月平均增长率为x，则可列方程为（ ）
| A． | 50（1+x）2=72 | B． | 50（1-x）2=72 | C． | 72（1-x）2=50 | D． | 50×2（1+x）=72 |
11．由四舍五入得到地球的半径约为6.4×103km，这个近似数的精确程度为（ ）
| A． | 1000km | B． | 100km | C． | 10km | D． | 1km |
15．已知反比例函数y=$\frac{k}{x}$的图象经过点P（-1，2），则这个函数的图象位于（ ）
| A． | 第一、三象限 | B． | 第二、三象限 | C． | 第二、四象限 | D． | 第三、四象限 |
5．
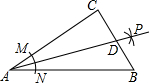如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（ ）
如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（ ）| A． | 30 | B． | 45 | C． | 60 | D． | 90 |
12．-6的绝对值与4的相反数的差，再加上-7，结果为（ ）
| A． | -5 | B． | -9 | C． | -3 | D． | 3 |
9．已知二次函数y=x2+bx+c（b、c为常数），若b+c=0，则它的图象经过的定点坐标为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （-1，1） | D． | （-1，-1） |
10．计算（a3b2）3÷（-a3）2的结果是（ ）
| A． | a6b2 | B． | a2b5 | C． | a5b3 | D． | a3b6 |