题目内容
13．将抛物线y=2x2先向上平移2个单位，再向右平移3个单位，则所得解析式是（ ）| A． | y=2（x-3）2+2 | B． | y=2（x-3）2-2 | C． | y=2（x+3）2-2 | D． | y=2（x+3）2+2 |
分析 先确定抛物线y=2x2的顶点坐标为（0，0），再把点（0，0）先向上平移2个单位，再向右平移3个单位后得到的点的坐标为（3，2），然后根据顶点式写出平移后抛物线的解析式．
解答 解：抛物线y=2x2的顶点坐标为（0，0），把点（0，0）先向上平移2个单位，再向右平移3个单位得到的点的坐标为（3，2），所以所得的抛物线的解析式为y=2（x-3）2+2．
故选：A．
点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
名校课堂系列答案
相关题目
3．“十二五”期间，将新建保障性住房约37000000套，用于解决中低收入和新参加工作的大学生住房的需求，把37000000用科学记数法表示应是（ ）
| A． | 37×106 | B． | 3.7×106 | C． | 3.7×107 | D． | 0.37×108 |
4．|-5-3|的相反数是（ ）
| A． | 8 | B． | -2 | C． | -8 | D． | 2 |
1．8362万用科学记数法表示为（ ）
| A． | 8.362×107 | B． | 83.62×108 | C． | 0.8362×107 | D． | 8.362×108 |
18．函数y=$\frac{k}{x}$的图象经过点A（1，-2），则k的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
5．
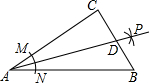如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（ ）
如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（ ）| A． | 30 | B． | 45 | C． | 60 | D． | 90 |
2．
如图，△ABC的周长为24，BC=10，BC边的垂直平分线交BC、AB于点D、E，则△AEC的周长是（ ）
如图，△ABC的周长为24，BC=10，BC边的垂直平分线交BC、AB于点D、E，则△AEC的周长是（ ）| A． | 16 | B． | 10 | C． | 19 | D． | 14 |
3．
如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点D的坐标为（ ）
如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点D的坐标为（ ）| A． | （3，3） | B． | （4，1） | C． | （3，1） | D． | （4，3） |