题目内容
10. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3)
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3)(1)若△ABC经过平移后得到△A1B1C1,点C1的坐标分别为(4,0),作出△A1B1C1的图形
(2)若△ABC和△A2B2C2关于原点O成中心对称,作出△A2B2C2的图形
(3)将△ABC绕着点O按逆时针方向旋转90°得到△A3B3C3,作出△A3B3C3的图形
(4)直接说明△A1B1C1和△A2B2C2是否成中心对称,若是直接写出对称中心的坐标.
分析 (1)根据点平移的坐标特征,利用点C平移到C1得到平移的规律,写出A1、B1的坐标,然后描点即可得到△A1B1C1;
(2)根据关于原点对称的点的坐标特征写出点A2、B2、C2,然后描点即可得到△A2B2C2;
(3)利用网格特点和旋转的性质画出点A3、B3、C3,然后描点即可得到△A3B3C3;
(4)利用画图可判定△A1B1C1和△A2B2C2是中心对称,然后写出对称中心的坐标.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)如图,△A3B3C3为所作;
(4)△A1B1C1和△A2B2C2是中心对称,对称中心的坐标为(2.5,-1.5).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换和平移变换.

练习册系列答案
相关题目
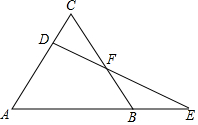 如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F. 如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星这一光明的象征联系在一起,请你画出这个对称图形的对称轴或对称中心.
如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星这一光明的象征联系在一起,请你画出这个对称图形的对称轴或对称中心.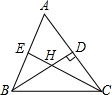 如图,在△ABC中,高BD,CE相交于H,已知∠HBC-∠HCB=10°,∠ABD=$\frac{1}{2}$∠HBC,求∠A的度数.
如图,在△ABC中,高BD,CE相交于H,已知∠HBC-∠HCB=10°,∠ABD=$\frac{1}{2}$∠HBC,求∠A的度数.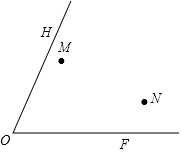 现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)
现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)