题目内容

4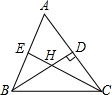．如图，在△ABC中，高BD，CE相交于H，已知∠HBC-∠HCB=10°，∠ABD=$\frac{1}{2}$∠HBC，求∠A的度数．

分析 设∠ABD=x，根据题意用x表示出∠ACE、∠DBC=2x、∠HCB，根据三角形内角和定理列出算式，求出x，计算即可．

解答 解：设∠ABD=x，
则∠ACE=x，∠DBC=2x，∠HCB=2x-10°，
在△BDC中，2x+2x-10°+x=90°，
解得，x=20°，
∴∠A=90°-∠ABD=70°．

点评 本题考查的是三角形内角和定理，掌握三角形内角和等于180°是解题的关键．

练习册系列答案
相关题目
9．能展开成如图所示的几何体名称是三棱柱．
10．如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（-3，5）、B（-2，1）、C（-1，3）
（1）若△ABC经过平移后得到△A1B1C1，点C1的坐标分别为（4，0），作出△A1B1C1的图形
（2）若△ABC和△A2B2C2关于原点O成中心对称，作出△A2B2C2的图形
（3）将△ABC绕着点O按逆时针方向旋转90°得到△A3B3C3，作出△A3B3C3的图形
（4）直接说明△A1B1C1和△A2B2C2是否成中心对称，若是直接写出对称中心的坐标．
7．据统计，宁波全市2014年实现地区生产总值7602.51亿元，同比增长7.6%．其中7602.51亿元用科学记数法可表示为（　　）
A．7.60251×1013元B．7.60251×1012元C．7.60251×1011元D．8.972031×1010元
14．解方程组：
（1）$\left\{\begin{array}{l}{3x-2y=8}\\{y+4x=7}\end{array}\right.$；（用代入法解）
（2）$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=2}\\{3x-4y=-7}\end{array}\right.$．（用加减法解）
9．百货商店服装柜在销售中发现：某品牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”国际儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．
（1）要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
（2）每件童装降价多少元时，每天销售这种童装的利润最高？最高利润是多少？
16．在平面直角坐标系中，O为坐标原点．
（1）已知点A（3，1），连结OA，作如下探究：
探究一：平移线段OA，使点O落在点B．设点A落在点C，若点B的坐标为（1，2），请在图1中作出BC，点C的坐标是（4，3）；
探究二：将线段OA绕点O逆时针旋转90°，点A落在点D．则点D的坐标是（-1，3）．
（2）已知四点O（0，0），A （a，b），C，B（c，d），顺次连结O，A，C，B．若所得到的四边形是正方形，请直接写出a，b，c，d应满足的关系式是a=d，b=-c或b=c，a=-d．
13．已知关于x的一元二次方程x2+ax+a-2=0．
（1）求证：不论a为何实数，此方程总有两个不相等的实数根．
（2）若该方程的两个实数根分别为x1，x2，且$|{x_1}-{x_2}|=\sqrt{13}$，求a的值．
14．计算
（1）$\sqrt{25}$-$\root{3}{-8}$+|-$\sqrt{2}$|；             
（2）2a•3a2+（-2a）3；
（3）（-2x）•（3x2-$\frac{1}{2}$x+2）；          
（4）（8a3-12a2b2）÷（2a）2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网