题目内容
15.合并同类项.(1)3x2+3x-6x2-2x+4;
(2)4a2+3b2+2ab-4a2-3b2;
(3)$\frac{1}{4}$a2b-0.4ab2-$\frac{1}{2}$a2b+$\frac{2}{5}$ab2-1.
分析 先找出同类项,再合并即可.
解答 解:(1)3x2+3x-6x2-2x+4
=(3-6)x2+(3-2)x+4
=-3x2+x+4;
(2)4a2+3b2+2ab-4a2-3b2
=(4-4)a2+(3-3)b2+2ab
=2ab;
(3)$\frac{1}{4}$a2b-0.4ab2-$\frac{1}{2}$a2b+$\frac{2}{5}$ab2-1
=($\frac{1}{4}$$-\frac{1}{2}$)a2b+(-0.4$+\frac{2}{5}$)ab2-1
=$-\frac{1}{2}$a2b-1.
点评 本题考查了同类项和合并同类项的应用,关键是把同类项的系数相加作为结果的系数,字母和字母的指数不变.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
3. 一志愿者在市中心某十字路口,对闯红灯的人次进行了统计,根据当天8:00-14:00中各阶段(以1小时为一时间段)闯红灯的人次制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别是( )
一志愿者在市中心某十字路口,对闯红灯的人次进行了统计,根据当天8:00-14:00中各阶段(以1小时为一时间段)闯红灯的人次制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别是( )
 一志愿者在市中心某十字路口,对闯红灯的人次进行了统计,根据当天8:00-14:00中各阶段(以1小时为一时间段)闯红灯的人次制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别是( )
一志愿者在市中心某十字路口,对闯红灯的人次进行了统计,根据当天8:00-14:00中各阶段(以1小时为一时间段)闯红灯的人次制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别是( )| A. | 30,30 | B. | 30,35 | C. | 35,40 | D. | 50,35 |
20. 如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )
如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )
 如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )
如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{3-\sqrt{5}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
 如图,分别作出已知图形关于给定直线l的对称图形.
如图,分别作出已知图形关于给定直线l的对称图形.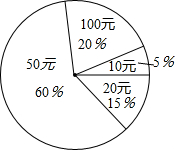 在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元.
在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元. 如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.
如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.