Question

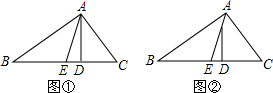
17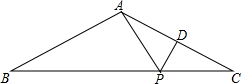．如图，在△ABC中，AB=AC，∠B=30°，点D是AC的中点，BC=6，点P是BC上一动点，求AP+PD的最小值．（提示：直角三角形中30°角所对的直角边等于斜边的一半）

Answer 1

分析 作A点关于BC的对称点A′，则AA′⊥BC，连接AD，交BC于P，此时PA+PD的值最小；AP+PD的最小值=A′D；根据等腰三角形的性质和等边三角形的性质以及直角三角函数即可求得A′D的值．

解答 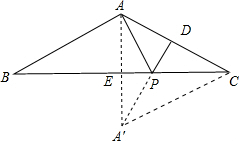解：作A点关于BC的对称点A′，则AA′⊥BC，连接AD，交BC于P，此时PA+PD的值最小；AP+PD的最小值=A′D；
∵AB=AC，
∴BE=CE=$\frac{1}{2}$BC=3，
∵∠B=30°，AB=AC，
∴∠B=∠C=30°，
∴∠BAC=120°，
∵AE⊥BC，
∴∠A′AC=∠A′AB=60°，
∴AE=tan30°•BE=$\frac{\sqrt{3}}{3}$×3=$\sqrt{3}$，AB=2AE，
∴AA′=AB=2$\sqrt{3}$，
∴AA′=AC，
∴△A′AC是等边三角形，
∵点D是AC的中点，
∴A′D⊥AC，
∴∠AA′D=30°，
∴A′D=cos30°•AA′=$\frac{\sqrt{3}}{2}$×$2\sqrt{3}$=3，
∴AP+PD的最小值为3．

点评 本题考查了轴对称-最短路线问题，等腰三角形的性质，等边三角形的判定和性质，解直角三角函数等，确定P点的位置是解题的关键．