题目内容
 如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=| 1 |
| 2 |
考点:三角形的面积
专题:阅读型
分析:过D点作AD⊥EF,交△ABC外侧两条直线于E、F,则EF=a,应用三角形的面积公式,根据S△ABC=S△ADB+S△ADC即可证得.
解答: 解:正确;
解:正确;
理由:过D点作AD⊥EF,交△ABC外侧两条直线于E、F,
∵过△ABC的三个顶点分别作出与水平线垂直的三条直线,
∴EF=a,
∵S△ADB=
AD•DE,S△ADC=
AD•DF,
∴S△ABC=S△ADB+S△ADC=
AD•DF+
AD•DE=
AD(DF+DE)=
AD•EF=
ah.
 解:正确;
解:正确;理由:过D点作AD⊥EF,交△ABC外侧两条直线于E、F,
∵过△ABC的三个顶点分别作出与水平线垂直的三条直线,
∴EF=a,
∵S△ADB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S△ADB+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的面积的求法,解决本题的关键是把所求的三角形面积合理分割,难点是准确得到相应线段长.

练习册系列答案
相关题目
下列各对数值是二元一次方程
x-y=6的解的是( )
| 1 |
| 2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
| A、y1<y2 |
| B、y1>y2 |
| C、y1≥y2 |
| D、y1≤y2 |
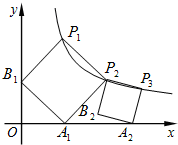 正方形的A1B1P1P2顶点P1、P2在反比例函数y=
正方形的A1B1P1P2顶点P1、P2在反比例函数y= 已知:△ABC内接正△DEF,AD=BF=CE,求证:△ABC为正三角形.
已知:△ABC内接正△DEF,AD=BF=CE,求证:△ABC为正三角形.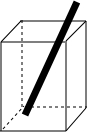 如图,将一根长为20cm的玻璃棒放入一个长为4cm,宽为3cm,高为12cm的长方形容器中,你知道玻璃棒露在外面的部分的长度d在什么范围之内吗?请通过计算写出d的范围.
如图,将一根长为20cm的玻璃棒放入一个长为4cm,宽为3cm,高为12cm的长方形容器中,你知道玻璃棒露在外面的部分的长度d在什么范围之内吗?请通过计算写出d的范围. 如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC,CD于点E,F.
如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC,CD于点E,F.