题目内容
9.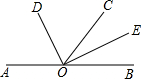 如图,O是直线AB上一点,OC是任一条射线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,O是直线AB上一点,OC是任一条射线,OD,OE分别是∠AOC,∠BOC的平分线.(1)请写出图中∠BOD的补角和∠BOE的余角;
(2)当∠BOE=25°时,求∠DOE和∠AOD的度数;
(3)图中有哪几对互补的角?
分析 (1)根据“和为180°的两个角互为补角”、“和为90°的两个角互为余角”进行解答;
(2)根据平角的定义和角平分线的定义进行求解.
(3)根据补角的定义进行解答.
解答 解:(1)∠DOB的补角:∠AOD、∠COD.
∠BOE的余角:∠AOD、∠COD;
(2)∵OE平分∠BOC,
∴∠BOC=2∠BOE=50°.
∴∠AOC=180°-∠BOC=130°.
∵OD平分∠AOC,
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC=65°.
∴∠DOE=∠COD+∠COE=65°+25°=90°;
(3)∠AOD和∠BOD互补,∠BOD和∠DOC互补,∠AOE和∠BOE互补,∠AOE和∠COE互补.
点评 此题考查了补角的概念、余角的概念、角平分线的定义.关键是掌握互余的角和为90°,互补的角和为180°.

练习册系列答案
相关题目
14.如果单项式-xa+1y3与12ybx2是同类项,那么a,b的值分别为( )
| A. | a=2,b=3 | B. | a=1,b=2 | C. | a=2,b=2 | D. | a=1,b=3 |
 如图,已知∠AOB=62°,∠1=(3x-2)°,∠2=(x+12)°,则∠1=37°.
如图,已知∠AOB=62°,∠1=(3x-2)°,∠2=(x+12)°,则∠1=37°.
 五子棋是一种两人对弈的棋类游戏,规则是:一方执黑子,一方执白子,由黑方先行,白方后行,在正方形棋盘中,双方交替下子,每次只能下一子,下在棋盘横线与竖线的交叉点上,最先在棋盘横向、竖向或斜向形成连续的相同颜色五个棋子的一方为胜,如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);此时轮到黑方下子,记其此步所下黑子为C,为了保证不让白方在两步之内(含两步)获胜,黑子C的坐标应该为(3,7)或(7,3).
五子棋是一种两人对弈的棋类游戏,规则是:一方执黑子,一方执白子,由黑方先行,白方后行,在正方形棋盘中,双方交替下子,每次只能下一子,下在棋盘横线与竖线的交叉点上,最先在棋盘横向、竖向或斜向形成连续的相同颜色五个棋子的一方为胜,如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);此时轮到黑方下子,记其此步所下黑子为C,为了保证不让白方在两步之内(含两步)获胜,黑子C的坐标应该为(3,7)或(7,3).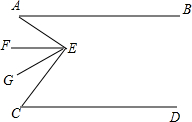 已知:如图,AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC,试判断EF和CD的位置关系,并说明理由.
已知:如图,AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC,试判断EF和CD的位置关系,并说明理由. 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D.若△ABC的周长为20cm,△BCE的周长为12cm,求BC的长.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D.若△ABC的周长为20cm,△BCE的周长为12cm,求BC的长.