题目内容
4.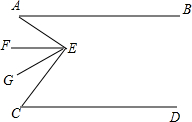 已知:如图,AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC,试判断EF和CD的位置关系,并说明理由.
已知:如图,AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC,试判断EF和CD的位置关系,并说明理由.
分析 先根据平行线的性质得:∠AHC=30°,由三角形内角和定理得:∠CEH=90°,由平角定理知:∠AEC=90°,由已知的三等分角得:∠CEF=∠ECD,根据平行线的判定定理证明结论.
解答 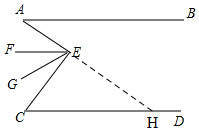 解:EF∥CD,理由是:
解:EF∥CD,理由是:
延长AE交CD于H,
∵AB∥CD,∠BAE=30°,
∴∠AHC=∠BAE=30°,
∵∠DCE=60°,
∴∠CEH=180°-∠AHC-∠DCE=180°-30°-60°=90°,
∴∠AEC=180°-∠CEH=180°-90°=90°,
∵EF、EG三等分∠AEC,
∴∠GEF=∠GEC=$\frac{1}{3}$∠AEC=30°,
∴∠CEF=∠GEF+∠GEC=30°+30°=60°,
∴∠CEF=∠ECD,
∴EF∥CD.
点评 本题考查的是平行线的性质和判定定理的综合运用,性质:两直线平行,同位角相等、内错角相等、同旁内角互补,判定:同位角相等、内错角相等、同旁内角互补,两直线平行.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
16.下列方程为一元一次方程的是( )
| A. | x+4=4-x2 | B. | x+y=-3x | C. | $\frac{1}{2x+3}=1$ | D. | 5-$\frac{1}{3}x=\frac{2}{3}x$ |
14.如图,点P在平面直角坐标系中按图中箭头方向运动,第一次从原点运动到点(1,1),第二次接着运动到点(2,0),第三次接着运动到点(3,2),…,按这样的运动规律,运动第2011次后的点坐标是 ( )
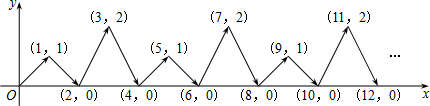

| A. | (2011,1) | B. | (2012,2) | C. | (2011,2) | D. | (2011,0) |
 如图是我市几个旅游景点的大致位置示意图,如果用(1,-1)表示新宁莨山的位置,用(2,4)表示隆回花瑶的位置,请在图中画出平面直角坐标系,并写出城市南山的坐标.
如图是我市几个旅游景点的大致位置示意图,如果用(1,-1)表示新宁莨山的位置,用(2,4)表示隆回花瑶的位置,请在图中画出平面直角坐标系,并写出城市南山的坐标.
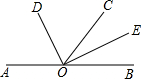 如图,O是直线AB上一点,OC是任一条射线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,O是直线AB上一点,OC是任一条射线,OD,OE分别是∠AOC,∠BOC的平分线.