题目内容
5.(1)知识再现如图(1):若点A,B在直线l同侧,A,B到l的距离分别是3和2,AB=4.现在直线l上找一点P,使AP+BP的值最小,做法如下:
作点A关于直线L的对称点A′,连接BA′,与直线l的交点就是所求的点P,线段BA′的长度即为AP+BP的最小值.请你求出这个最小值.
(2)实践应用
①如图(2),⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是2$\sqrt{3}$;
②如图(3),Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.
③如图(4),菱形ABCD中AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\sqrt{3}$.
④如图(5),在R△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
(3)拓展延伸
如图(6),在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留作图痕迹,不必写出作法.
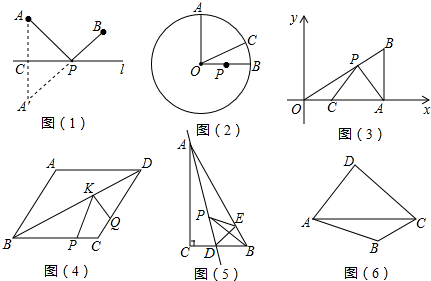
分析 (1)如图1中,作BM⊥AA′于M,连接AB,在RT△ABM中利用勾股定理求出BM2,再在RT△BMA′中利用勾股定理即可解决问题.
(2)①如图2中,延长AO交⊙O于H,连接CH交OB于点P,此时PA+PC最小,利用勾股定理计算即可.
②如图3中,在y轴上取一点C′使得OC′=0C=1,连接AC′交OB于点P,此时PC+PA最小,最小值=AC′,利用勾股定理计算即可.
③如图4中,当KP⊥BC,KQ⊥CD时,KP+KQ最小,利用$\frac{1}{2}$•BD•CO=$\frac{1}{2}$•BC•KP+$\frac{1}{2}$•CD•KQ,即可解决问题.
④如图5中,因为E、C关于AD对称,所以当点P与点D重合时,△PEB周长最小,利用勾股定理计算即可.
(3)作点B关于AC的对称点B′,连接DB′并延长交AC于点P,此时∠APB=∠DPA.
解答 解:(1)如图1中,作BM⊥AA′于M,连接AB.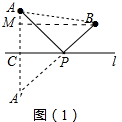
在RT△BMA中,∵∠BMA=90°,AB=4,AM=1,
∴BM2=AB2-AM2=15,
在RT△BMA′中,∵∠BMA′=90°,MA′=5,
∴BA′=$\sqrt{B{M}^{2}+MA{′}^{2}}$=$\sqrt{15+25}$=2$\sqrt{10}$.
(2)①如图2中,延长AO交⊙O于H,连接CH交OB于点P,此时PA+PC最小,
∵OA=OH,PO⊥AH,
∴PA=PH,
∴PA+PC=PH+PC=HC,
∵AH是直径,
∴∠ACH=90°,∵∠AOC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠HAC=60°,
在RT△ACH中,∵∠AHC=30°,AC=2,
∴AH=4,CH=$\sqrt{A{H}^{2}-A{C}^{2}}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
②如图3中,作点C关于直线OB的对称点C′,连接AC′交OB于点P,此时PC+PA最小,最小值=AC′,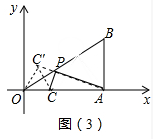
∵点C′坐标($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)
∴AC′=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{5}{2})^{2}}$=$\sqrt{7}$,
故答案为$\sqrt{7}$.
③如图4中,当KP⊥BC,KQ⊥CD时,KP+KQ最小,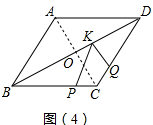
连接AC交BD于点O,由题意:$\frac{1}{2}$•BD•CO=$\frac{1}{2}$•BC•KP+$\frac{1}{2}$•CD•KQ,
∴KP+KQ=$\sqrt{3}$,
故答案为$\sqrt{3}$.
④如图5中,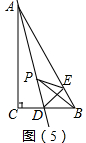
∵E、C关于AD对称,
∴当点P与点D重合时,△PEB周长最小,
在RT△DEB中,∵∠DEB=90°,DE=CD=$\sqrt{3}$,∠DBE=60°,
∴BD=2EB,设EB=x,则BD=2x,
∴(2x)2=x2+($\sqrt{3}$)2,
∴x=±1,
∵x>0,
∴x=1,
∴EB=1,DB=2,
∴△PEB周长最小值=3+$\sqrt{3}$.
故答案为3+$\sqrt{3}$.
(3)作点B关于AC的对称点B′,连接DB′并延长交AC于点P,此时∠APB=∠DPA.
点评 本题考查圆的综合题、最短问题、勾股定理、面积法、两点之间线段最短等知识,解题的关键是利用轴对称解决最值问题,灵活运用两点之间线段最短解决问题,所以中考常考题型.

| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
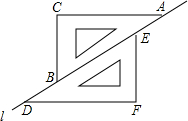 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )| A. | BD=AE | B. | CB=BF | C. | BE⊥CF | D. | BA平分∠CBF |
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
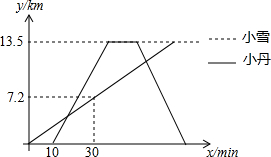 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km. 如图,在?ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.
如图,在?ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形. 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.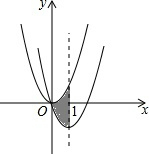 如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.
如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.