题目内容
6.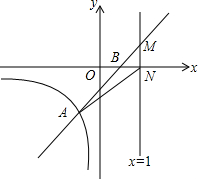 直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0)
直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0)(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=$\frac{3}{2}$,求t的值.
分析 (1)将点A坐标代入y=$\frac{2}{x}$可得m的值;
(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;
(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN=$\frac{3}{2}$可得关于t的方程,解方程可得t的值.
解答 解:(1)将点A(-1,m)代入y=$\frac{2}{x}$,得:m=-2;
(2)由(1)知点A坐标为(-1,-2),
将点A(-1,-2)、B(1,0)代入y=kx+b,
得:$\left\{\begin{array}{l}{-k+b=-2}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为:y=x-1;
(3)当x=t时,y=t-1,
∴点M坐标为(t,t-1),点N坐标为(t,0),
∵S△AMN=$\frac{3}{2}$,
∴$\frac{1}{2}$×(t-1)(t+1)=$\frac{3}{2}$,
解得:t=2或t=-2(舍),
∴t=2.
点评 此题考查了一次函数与反比例函数的交点问题,以及坐标与图形性质,熟练掌握待定系数法求函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某公司全体员工年薪的具体情况如表:
则该公司全体员工年薪制的中位数比众数多0.5万元.
| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 | 3 |
| 员工数/人 | 1 | 2 | 3 | 4 | 5 | 6 | 4 |
15.某射击队要从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
小明根据统计结果计算了甲的平均数和方差,方法如下:
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
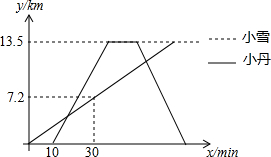 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km. 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.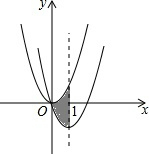 如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.
如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1. 如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.
如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.