题目内容
4. 如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E.
如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E.(1)求k的值;
(2)若第一象限的双曲线y=$\frac{m}{x}$与△BDE没有交点,请直接写出m的取值范围.
分析 (1)过点B作BM⊥OA于点M,由等边三角形的性质结合点A的坐标找出点B的坐标,再利用中点坐标公式即可求出点D的坐标,最后利用待定系数法即可得出结论;
(2)设过点B的反比例函数的解析式为y=$\frac{n}{x}$,由点B的坐标利用待定系数法求出n的值,根据反比例函数的性质即可得出m的取值范围.
解答 解:(1)过点B作BM⊥OA于点M,如图所示.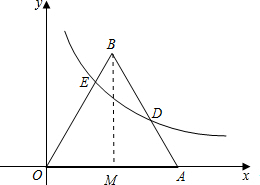
∵点A(4$\sqrt{3}$,0),
∴OA=4$\sqrt{3}$,
又∵△ABO为等边三角形,
∴OM=$\frac{1}{2}$OA=2$\sqrt{3}$,BM=$\frac{\sqrt{3}}{2}$OA=6.
∴点B的坐标为(2$\sqrt{3}$,6).
∵点D为线段AB的中点,
∴点D的坐标为($\frac{2\sqrt{3}+4\sqrt{3}}{2}$,$\frac{6}{2}$)=(3$\sqrt{3}$,3).
∵点D为函数y=$\frac{k}{x}$(x>0,k为常数)的图象上一点,
∴有3=$\frac{k}{3\sqrt{3}}$,解得:k=9$\sqrt{3}$.
(2)设过点B的反比例函数的解析式为y=$\frac{n}{x}$,
∵点B的坐标为(2$\sqrt{3}$,6),
∴有6=$\frac{n}{2\sqrt{3}}$,解得:n=12$\sqrt{3}$.
若要第一象限的双曲线y=$\frac{m}{x}$与△BDE没有交点,只需0<m<k或m>n即可,
∴0<m<9$\sqrt{3}$或m>12$\sqrt{3}$.
答:若第一象限的双曲线y=$\frac{m}{x}$与△BDE没有交点,m的取值范围为0<m<9$\sqrt{3}$或m>12$\sqrt{3}$.
点评 本题考查了反比例函数的性质、中点坐标公式、等边三角形的性质以及待定系数法求反比例函数的解析式,解题的关键是:(1)求出点D的坐标;(2)求出过点B的反比例函数的系数.本题属于基础题,难度不大,解决该题型题目时,利用等边三角形的性质结合中点坐标公式求出反比例函数图象上一点的坐标,再利用待定系数法求出反比例函数的系数即可.

 阅读快车系列答案
阅读快车系列答案| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
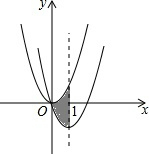 如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.
如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.
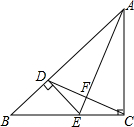 已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④.
已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④. 如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.
如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.