题目内容
9.已知三角形三个内角的度数之比为2:2:5,则其最大内角的度数是 100°.分析 首先设三角形三个内角度数为2x°,2x°,5x°,根据三角形内角和定理可得2x+2x+5x=180,解方程可得x的值,进而可得答案.
解答 解:设三角形三个内角度数为2x°,2x°,5x°,由题意得:
2x+2x+5x=180,
解得:x=20,
5x°=100°,
故答案为:100°.
点评 此题主要考查了三角形内角和定理,关键是掌握三角形内角和是180°.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
4.在△ABC中,AD是∠BAC的平分线,若∠B=50°,∠C=70°,则∠CAD的度数是( )
| A. | 15° | B. | 30° | C. | 60° | D. | 120° |
16.1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此下去,第6次后剩下的小棒长为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{128}$ |
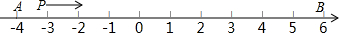 如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).
如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).