题目内容
16.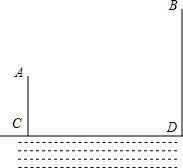 如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
分析 作点A关于CD的对称点E,连结BE交CD于点O,如图,根据对称的性质得OA=OE,AC=CE=1,则OA+OB=OE+OB=BE,根据两点之间线段最短得到此时点O使OA+OB最小,设OC=xkm,则OD=(3-x)km,再证明△ECO∽△BDO,利用相似比得$\frac{x}{3-x}$=$\frac{1}{3}$,然后利用比例性质求出x即可.
解答 解: 作点A关于CD的对称点E,连结BE交CD于点O,如图,
作点A关于CD的对称点E,连结BE交CD于点O,如图,
∵点A关于CD的对称点E,
∴OA=OE,AC=CE=1,
∴OA+OB=OE+OB=BE,
∴此时点O使OA+OB最小,
设OC=xkm,则OD=(3-x)km,
∵CE∥BD,
∴△ECO∽△BDO,
∴$\frac{CO}{OD}$=$\frac{CE}{BD}$,即$\frac{x}{3-x}$=$\frac{1}{3}$,解得x=1.5(km).
答:在CD上选择在离C处1.5km的地方建水厂,使铺设的水管总长度最小.
点评 本题考查了相似三角形的应用:用相似三角形对应边的比相等的性质求物体的长度.也考查了最短路径问题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
6.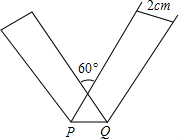 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )| A. | $\frac{2}{3}$$\sqrt{3}$cm | B. | $\frac{4}{3}$$\sqrt{3}$cm | C. | $\sqrt{5}$cm | D. | 2cm |

 已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将
已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将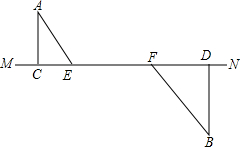 如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y.
如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y. 如图,已知正方形ABCD的边长为3,如果将线段AC绕点A旋转后,点C落在BA延长线上的C′点处,那么tan∠ADC′=$\sqrt{2}$.
如图,已知正方形ABCD的边长为3,如果将线段AC绕点A旋转后,点C落在BA延长线上的C′点处,那么tan∠ADC′=$\sqrt{2}$. 如图,在Rt△ABC中,AB=AC=2$\sqrt{2}$.∠BAC=90°,以A为圆心1为半径作圆,O为BC上的一动点,以O为圆心OB为半径作圆.若⊙0与⊙A相切,求0B的长.
如图,在Rt△ABC中,AB=AC=2$\sqrt{2}$.∠BAC=90°,以A为圆心1为半径作圆,O为BC上的一动点,以O为圆心OB为半径作圆.若⊙0与⊙A相切,求0B的长.