题目内容
11.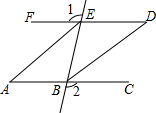 如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.(1)求证:AB∥DE;
(2)BD平分∠EBC吗?为什么?
分析 (1)先根据对顶角相等得出∠2=∠ABE,再由∠1=∠2可知∠1=∠ABE,根据平行线的判定定理即可得出结论;
(2)根据(1)中AB∥CD可知∠AED+∠BAE=180°,∠BEF=∠EBC,根据∠BAE=∠BDE可得∠AED+∠BDE=180°,故AE∥BD,所以∠AEB=∠DBE,再根据EA平分∠BEF可得出结论.
解答 (1)证明:∵∠2与∠ABE是对顶角,
∴∠2=∠ABE.
∵∠1=∠2,
∴∠1=∠ABE,
∴AB∥DE;
(2)解:BD平分∠EBC.
理由:∵由(1)知AB∥CD,
∴∠AED+∠BAE=180°,∠BEF=∠EBC.
∵∠BAE=∠BDE,
∴∠AED+∠BDE=180°,
∴AE∥BD,
∴∠AEB=∠DBE.
∵EA平分∠BEF,∠BEF=∠EBC,
∴BD平分∠EBC.
点评 本题考查的是平行线的判定与性质,先根据同位角相等判断出AB∥CD是解答此题的关键.

练习册系列答案
相关题目
2.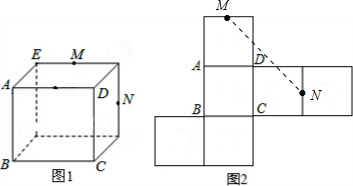 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )| A. | 11$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 10 | D. | 8 |
20.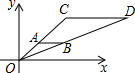 如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )
如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )
 如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )
如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )| A. | (4,2) | B. | (6,3) | C. | (8,4) | D. | (8,3) |
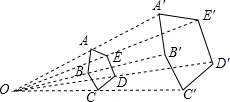 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.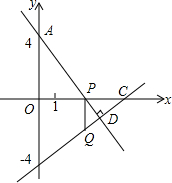 如图,在平面直角坐标系中,A,B两点的坐标分别是(0,4),(0,-4). 点P(p,0)是x轴上一个动点,过点B作直线BC⊥AP于点D,过点P作PQ∥y轴,交BC于点Q. 当p≠0时,直线BC与x轴交于点C.
如图,在平面直角坐标系中,A,B两点的坐标分别是(0,4),(0,-4). 点P(p,0)是x轴上一个动点,过点B作直线BC⊥AP于点D,过点P作PQ∥y轴,交BC于点Q. 当p≠0时,直线BC与x轴交于点C.