题目内容
20.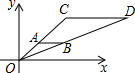 如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )
如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )| A. | (4,2) | B. | (6,3) | C. | (8,4) | D. | (8,3) |
分析 利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵A点的坐标为(1,1),C点的坐标为(3,3),
∴位似比k=3,
∵B点的坐标为(2,1),
∴点D的坐标是:(2×3,1×3 ),即(6,3).
故选:B.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.现有两种不同型号的手机和四种不同型号的手机套,其中有两种型号的手机套分别能套上这两种型号手机,任意取出一个手机套去套任意一手机,一次就能套上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
5.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-4)^{2}}$=-4 | C. | ($\sqrt{2}$)2=2 | D. | (2$\sqrt{3}$)2=6 |
12.某校羽毛球训练队共有8名队员,他们的年龄(单位:岁)分别为:12、13、13、14、12、13、15、13,则他们年龄的众数、极差分别是( )
| A. | 12,3 | B. | 13,3 | C. | 14,2 | D. | 13,2 |
 已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点
已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点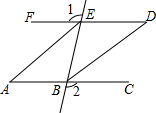 如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.