题目内容
3.如果一条弧长等于$\frac{π}{4}$R,它的半径是R,那么这条弧所对的圆心角度数为45°,当圆心角增加30°时,这条弧长增加$\frac{1}{6}$πR.分析 根据弧长公式l=$\frac{nπr}{180}$,列出方程求出这条弧所对的圆心角度数;圆心角增加30°时,圆心角为45°+30°=75°,直接代入公式求出即可.
解答 解:设这条弧所对的圆心角度数为n,
依题意有$\frac{nπR}{180}$=$\frac{π}{4}$R,
解得n=45.
45°+30°=75°,
圆心角增加30°时,这条弧长为$\frac{75πR}{180}$=$\frac{5πR}{12}$;
$\frac{5πR}{12}$-$\frac{π}{4}$R=$\frac{1}{6}$πR,
故答案为:45°,$\frac{1}{6}$πR.
点评 本题主要考查了弧长公式,熟练记忆弧长公式是解题关键

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.一个菱形的周长是20,两条对角线之比是4:3,则这个菱形的面积是( )
| A. | 25 | B. | 24 | C. | 12 | D. | 7 |
8.现有两种不同型号的手机和四种不同型号的手机套,其中有两种型号的手机套分别能套上这两种型号手机,任意取出一个手机套去套任意一手机,一次就能套上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
12.某校羽毛球训练队共有8名队员,他们的年龄(单位:岁)分别为:12、13、13、14、12、13、15、13,则他们年龄的众数、极差分别是( )
| A. | 12,3 | B. | 13,3 | C. | 14,2 | D. | 13,2 |
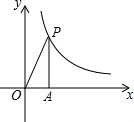 如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求:
如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求: 在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指 (填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).
在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指 (填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).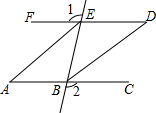 如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.