题目内容

1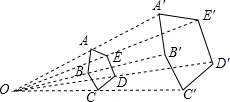．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形，A′B′C′D′E′，已知OA=10cm，OA′=20cm，五边形ABCDE的周长为15cm，则五边形A′B′C′D′E′的周长为30cm．

分析 由以点O为位似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，OA=10cm，OA′=20cm，可得五边形ABCDE的周长与五边形A′B′C′D′E′的位似比为：10：20=1：2，然后由相似多边形的性质可证得：五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是：1：2．

解答 解：∵以点O为位似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，OA=10cm，OA′=20cm，
∴五边形ABCDE的周长与五边形A′B′C′D′E′的位似比为：10：20=1：2，
∴五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是：1：2，
故五边形A′B′C′D′E′的周长为：30cm．
故答案为：30．

点评 此题考查了位似图形的性质．此题难度不大，注意相似多边形的周长比等于相似比．

练习册系列答案
相关题目
11．下列一元二次方程中，没有实数根的是（　　）
A．x2-3x-l=0B．x2-1=0C．x2-2x+l=0D．x2+2x+3=0
12．$\left\{\begin{array}{l}{x=2}\\{y=7}\end{array}\right.$是方程ax-3y=2的一个解，则a为（　　）
A．8B．$\frac{23}{2}$C．-$\frac{23}{2}$D．-$\frac{19}{2}$
9．在等边△ABC的两边AB、AC所在直线上分别有两点M、N．D为△ABC外一点，且∠MDN=60°，∠BDC=120°，BD=DC． 探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系．

（1）如图1所示，当点M、N在边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系是BM+NC=MN； 此时$\frac{Q}{L}$=$\frac{2}{3}$；（不必证明）
（2）如图2所示，点M、N在边AB、AC上，且当DM≠DN时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明；
（3）如图3所示，当M、N分别在边AB、CA的延长线上时，若AN=2，则Q=4+$\frac{2}{3}$L（用含有L的式子表示）．
16．已知关于x的一元二次方程3x2+mx-2=0的一个解与方程$\frac{5}{x-3}$=$\frac{2}{x}$的解相同．
（1）解方程：$\frac{5}{x-3}$=$\frac{2}{x}$；
（2）求m的值，并求出方程3x2+mx-2=0的另一个解．
6．抛物线y=x2+4x+4的对称轴是（　　）
A．直线x=4B．直线x=-4C．直线x=2D．直线x=-2
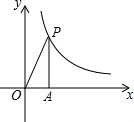13．如图，已知点P（x，y）是反比例函数图象上一点，O是坐标原点，PA⊥x轴，S△PAO=4，且图象经过（1，3m-1）；求：
（1）反比例函数解析式．
（2）m的值．
10．已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点，另一直线经过点B和点
D（11，6）．
（1）求A、B的坐标；
（2）证明：△ABD是直角三角形；
（3）在x轴上找点C，使△ACD是以AD为底边的等腰三角形，求出C点坐标．
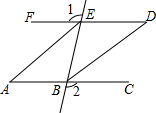11．如图，∠1=∠2，∠BAE=∠BDE，EA平分∠BEF．
（1）求证：AB∥DE；
（2）BD平分∠EBC吗？为什么？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网