题目内容
2.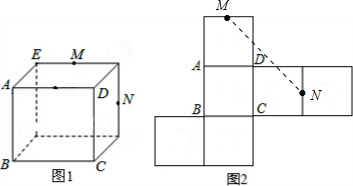 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )| A. | 11$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 10 | D. | 8 |
分析 如图2,作辅助线;运用勾股定理直接求出MN的长度,即可解决问题.
解答  解:如图2,连接MN,分别延长正方形的边交于点P;
解:如图2,连接MN,分别延长正方形的边交于点P;
则△MPN为直角三角形,
由题意得:MP=NP=5+6=11,
由勾股定理得$MN=\sqrt{1{1}^{2}+1{1}^{2}}=11\sqrt{2}$.
故选A.
点评 该题主要考查了几何体的展开图、勾股定理的应用等问题;解题的关键是能够在展开图中作出线段MN,灵活运用勾股定理来分析、判断、解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.$\left\{\begin{array}{l}{x=2}\\{y=7}\end{array}\right.$是方程ax-3y=2的一个解,则a为( )
| A. | 8 | B. | $\frac{23}{2}$ | C. | -$\frac{23}{2}$ | D. | -$\frac{19}{2}$ |
7.下列计算,正确的是( )
| A. | 3x2+2x2=6x2 | B. | x3•x2=x6 | C. | x3÷x2=x | D. | (2x2)3=6x6 |
12.某校羽毛球训练队共有8名队员,他们的年龄(单位:岁)分别为:12、13、13、14、12、13、15、13,则他们年龄的众数、极差分别是( )
| A. | 12,3 | B. | 13,3 | C. | 14,2 | D. | 13,2 |
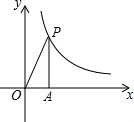 如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求:
如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求: 已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点
已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点 在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指 (填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).
在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指 (填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).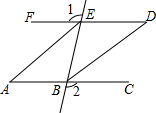 如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.