题目内容
3.在△ABC中,点D、E分别在边AB、AC上,如果AD=2,BD=4,那么由下列条件能够判断DE∥BC的是( )| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}=\frac{1}{3}$ | C. | $\frac{AE}{AC}=\frac{1}{3}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
分析 先求出比例式,再根据相似三角形的判定得出△ADE∽△ABC,根据相似推出∠ADE=∠B,根据平行线的判定得出即可.
解答 解:
只有选项C正确,
理由是:∵AD=2,BD=4,$\frac{AE}{AC}$=$\frac{1}{3}$,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{3}$,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC,
根据选项A、B、D的条件都不能推出DE∥BC,
故选C.
点评 本题考查了平行线分线段成比例定理,相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
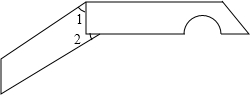 如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.
如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°. 如图,为测量池塘的宽AB,先在池塘外选一点O,连接AO、BO,测得AO=18cm,BO=21cm,再延长AO、BO分别到C、D两点,使OC=6cm,OD=7cm,若测得CD=5cm,则池塘宽AB等于( )
如图,为测量池塘的宽AB,先在池塘外选一点O,连接AO、BO,测得AO=18cm,BO=21cm,再延长AO、BO分别到C、D两点,使OC=6cm,OD=7cm,若测得CD=5cm,则池塘宽AB等于( )

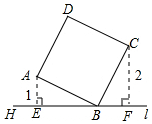 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm.
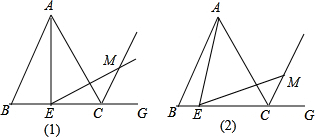
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm. 如图,△ABC中,AB=5,AC=4,BD平分∠ABC,CD平分∠ACB,过点D作BC的平行线,交AB于点M,将AC于点N,则△AMN的周长为9.
如图,△ABC中,AB=5,AC=4,BD平分∠ABC,CD平分∠ACB,过点D作BC的平行线,交AB于点M,将AC于点N,则△AMN的周长为9.