题目内容
11.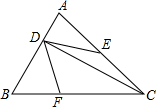 如图,在△ABC中,∠B=60°,CD为AB边上的高,E为AC边的中点,点F在BC边上,∠EDF=60°,若BF=3,CF=5,则AC边的长为2$\sqrt{13}$.
如图,在△ABC中,∠B=60°,CD为AB边上的高,E为AC边的中点,点F在BC边上,∠EDF=60°,若BF=3,CF=5,则AC边的长为2$\sqrt{13}$.
分析 过D作DM⊥BC于M,根据直角三角形的性质得到BD=$\frac{1}{2}$BC=4,得到DM=2$\sqrt{3}$,BM=2,MF=1,DF=$\sqrt{13}$,取BC的中点H,连接DH,EH,根据三角形的中位线的性质得到EH∥AB,根据平行线的性质得到∠EHD=60°,根据相似三角形的性质即可得到结论.
解答 解:过D作DM⊥BC于M,
∵CD为AB边上的高,
∴∠CDB=90°,
∵∠B=60°,
∴BD=$\frac{1}{2}$BC=4,
∴DM=2$\sqrt{3}$,BM=2,
∴MF=1,DF=$\sqrt{13}$,
取BC的中点H,连接DH,EH,
∵E为AC边的中点,
∴EH∥AB,
∴∠EHD=60°,
∵∠BDH=60°,∠EDF=60°,
∴∠BDF=∠HDE,
∴△BDF∽△HDE,
∴$\frac{BD}{DF}=\frac{DH}{DE}$,
∴$\frac{4}{\sqrt{13}}$=$\frac{4}{DE}$,
∴DE=$\sqrt{13}$,
∴AC=2$\sqrt{13}$.
故答案为:2$\sqrt{13}$.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,三角形中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
12.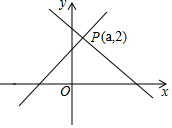 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
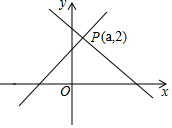 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )| A. | x≥-1 | B. | 0≤x≤1 | C. | x≥1 | D. | x≤1 |
6.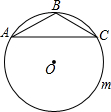 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
 如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.
如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.