题目内容
11.已知AB、CD是⊙O的两条直径,则四边形ACBD一定是矩形.分析 根据圆的直径相等,且圆心为直径的中点,得到圆心到A、B、C及D四点的距离相等,根据对角线互相平分且对角线相等,得到四边形ACBD为矩形.
解答  解:连接AC、BC、BD、AD,
解:连接AC、BC、BD、AD,
∵AB、CD为圆O的直径,
∴OA=OB=OC=OD,
∴四边形ACBD为矩形.
故答案是:矩.
点评 此题考查圆周角定理和矩形的判别方法,考查了数形结合的数学思想,是一道基础题.

练习册系列答案
相关题目
16.定义两种新运算“△”和“*”,a△b=a2-ab,a*b=3a-b2,则($\sqrt{2}$△1)△($\frac{\sqrt{2}}{3}$*$\sqrt{2}$)的值为( )
| A. | 8+12$\sqrt{2}$ | B. | 8-12$\sqrt{2}$ | C. | 12+8$\sqrt{2}$ | D. | 12-8$\sqrt{2}$ |
20.下列说法正确的是( )
| A. | 平方根等于本身的数是0 | |
| B. | $\sqrt{36}$表示6的算术平方根 | |
| C. | 无限小数都是无理数 | |
| D. | 数轴上的每一个点都表示一个有理数 |
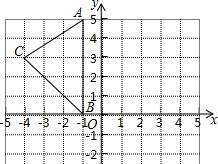 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1点关于x轴对称的点的坐标.
如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1点关于x轴对称的点的坐标. 已知数a,b,c在数轴上的位置如图所示,化简|a+2b|-|c-2b|的结果是a+c.
已知数a,b,c在数轴上的位置如图所示,化简|a+2b|-|c-2b|的结果是a+c.