题目内容
10．
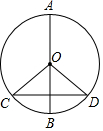已知：如图，⊙O的半径是6cm，∠BOD=30°，$\widehat{BD}$=$\widehat{BC}$，求CD的长．
分析 根据$\widehat{BD}$=$\widehat{BC}$得出AB⊥CD，故CD=2DE，再由直角三角形的性质得出DE的长，进而可得出结论．
解答 
解：∵$\widehat{BD}$=$\widehat{BC}$，
∴AB⊥CD，
∴CD=2DE．
∵⊙O的半径是6cm，∠BOD=30°，
∴DE=$\frac{1}{2}$OD=3cm，
∴CD=6cm．
点评 本题考查的是圆心角、弧、弦的关系，熟知在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等是解答此题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
20．
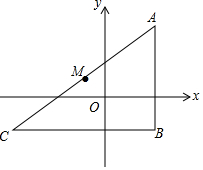如图，在Rt△ABC中，∠B=90°，AB垂直于x轴，M为AC的中点，若点A的坐标为（3，4），点M的坐标为（-1，1），则点B的坐标为（ ）
如图，在Rt△ABC中，∠B=90°，AB垂直于x轴，M为AC的中点，若点A的坐标为（3，4），点M的坐标为（-1，1），则点B的坐标为（ ）| A． | （3，-4） | B． | （3，-3） | C． | （3，-2） | D． | （3，-1） |
如图，直线y=x-$\sqrt{2}$与x轴、y轴分别交于A、B两点，与反比例函数的图象交于C、D两点，已知AO=AC．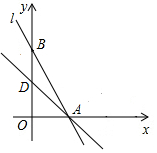
已知如图，在平面直角坐标系中，直线AB分别与x轴、y轴交于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x2-18x+72=0的两根，点D为线段OB的中点，过点D作AB的垂线与线段AB相交于点C．
2．将代数式x4+x2加上一个单项式后，其结果是一个代数式的完全平方．则这样的单项式有（ ）个．
| A． | 6 | B． | 5 | C． | 4 | D． | 不超过3 |
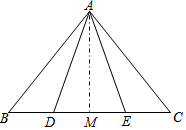已知点D、E在△ABC的BC边上，AD=AE，BD=CE，为了判断∠B与∠C的大小关系，请你填空完成下面的推理过程，并在空白括号内，注明推理的根据．