题目内容
6．
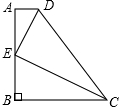如图，已知CB⊥AB，点E在AB上，且CE平分∠BCD，DE平分∠ADC，∠EDC+∠DCE=90°，求证：DA⊥AB．
分析 根据角平分线的定义可得∠ADC=2∠EDC，∠BCD=2∠DCE，然后求出∠ADC+∠BCD=180°，根据同旁内角互补，两直线平行可得AD∥BC，再根据两直线平行，同旁内角互补证明即可．
解答 证明：∵DE、CE分别平分∠ADC、∠BCD，
∴∠ADC=2∠EDC，∠BCD=2∠DCE，
∵∠EDC+∠DCE=90°，
∴∠ADC+∠BCD=2×90°=180°，
∴AD∥BC，
又∵CB⊥AB，
∴∠B=90°，
∴∠A=180°-90°=90°，
∴AB⊥DA．
点评 本题考查了角平分线的定义，平行线的判定与性质，以及垂直的定义，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
14．甲、乙两个搬运工搬运某种货物，已知乙比甲每小时多搬运600kg，甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等，求甲、乙两人每小时分别搬运多少kg货物．设甲每小时搬运xkg货物，则可列方程为（ ）
| A． | $\frac{5000}{x-600}$=$\frac{8000}{x}$ | B． | $\frac{5000}{x+600}$=$\frac{8000}{x}$ | C． | $\frac{5000}{x}$=$\frac{8000}{x+600}$ | D． | $\frac{5000}{x}$=$\frac{8000}{x-600}$ |