题目内容
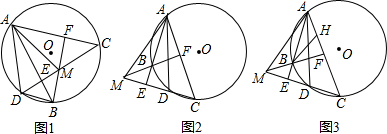
17.已知AB、CD是⊙O的两条弦,直线AB、CD互相垂直,垂足为E,连接AC,过点B作BF⊥AC,垂足为F,直线BF交直线CD于点M.(1)如图1,当点E在⊙O内时,连接AD,AM,BD,求证:AD=AM;
(2)如图2,当点E在⊙O外时,连接AD,AM,求证:AD=AM;
(3)如图3,当点E在⊙O外时,∠ABF的平分线与AC交于点H,若tan∠C=$\frac{4}{3}$,求tan∠ABH的值.
分析 (1)根据垂直的定义和垂直平分线的判定好小子即可求解;
(2)如图2,连结BD,先证明四边形ABDC是圆内接四边形,根据圆内接四边形的性质和垂直平分线的性质即可求解;
(3)如图3,过点H作HN⊥AB,垂足为N,在Rt△ABF中和在Rt△BNH中,根据三角函数的定义即可求解.
解答 (1)证明:∵AB⊥CD,BF⊥AC,
∴∠BEM=∠BFA=90°,
∴∠EBM+∠BME=90°,∠ABF+∠BAF=90°,
∴∠BME=∠BAC,
∴∠BDM=∠BMD,
∴BD=BM,
∵AB⊥CD,
∴AB是MD的垂直平分线,
∴AD=AM; (2)证明:如图2,连结BD,
(2)证明:如图2,连结BD,
∵AB⊥CD,BF⊥AC,
∴∠BEM=∠BFA=90°,
∵∠EBM=∠FBA,
∴∠BME=∠BAF,
∴四边形ABDC是圆内接四边形,
∴∠BDM=∠BAC,
∴∠BDM=∠BMD,
∴BD=BM,
∵AB⊥CD,
∴AB是MD的垂直平分线,
∴AD=AM; (3)解:如图3,过点H作HN⊥AB,垂足为N.
(3)解:如图3,过点H作HN⊥AB,垂足为N.
易知∠AHN=∠ABF=∠C,
在Rt△ANH中,设HN=3m,
∵tan∠AHN=tan∠C=$\frac{AN}{NH}$=$\frac{4}{3}$,
∴AN=4m,
∴AH=5m,
∵BH平分∠ABF,
∴HN=HF=3m,
∴AF=AH+HF=8m,
在Rt△ABF中,∵tan∠ABF=tan∠C=$\frac{AF}{BF}$=$\frac{4}{3}$,
∴BF=6m,
∴AB=10m,
∴BN=AB-AN=6m,
∴在Rt△BNH中,tan∠NBH=$\frac{NH}{BN}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴tan∠ABH=$\frac{1}{2}$.
点评 本题考查了圆的综合,涉及了圆内接四边形的判定与性质、等腰三角形的判定与性质及垂直平分线的性质,三角函数,解答本题的关键是掌握数形结合思想运用.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | -1 | B. | 1 | C. | 3 | D. | -4 |
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写表格:
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 8 | 0.4 |
| 乙 | 8 | 9 | 9 | 3.2 |
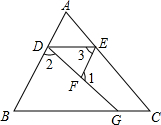 如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.
如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.