题目内容
2.观察下列等式,找出规律然后空格处填上具体的数字.1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
1+3+5+7+9+11=36=62.
根据规律填空:1+3+5+7+9+…+99=2500=502.
分析 根据已知等式知,从1开始的连续n个奇数的和等于序数加1和的平方,据此可知第49个等式的和为502,第n个等式的和为(n+1)2.
解答 解:∵第1个等式:1+3=4=22;
第2个等式:1+3+5=9=32;
第3个等式:1+3+5+7=16=42;
第4个等式:1+3+5+7+9=25=52;
…
∴第5个等式:1+3+5+7+9+11=36=62
第n个等式:1+3+5+7+9+…+(2n+1)=(n+1)2,
当2n+1=99,即n=49时,1+3+5+7+…+99=502=2500,
故答案为:36,62,2500,502.
点评 本题主要考查数字的变化规律,根据已知等式发现规律并会用代数式表示是关键.

练习册系列答案
相关题目
11.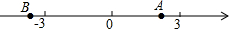 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
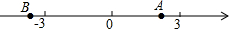 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )| A. | 甲、乙 | B. | 丙、丁 | C. | 甲、丙 | D. | 乙、丁 |
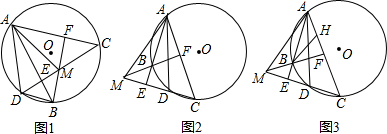
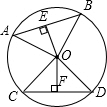 如图,AB,CD是⊙O的两条弦.
如图,AB,CD是⊙O的两条弦.