题目内容
8. 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点D从B出发向A运动,作
如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点D从B出发向A运动,作DE⊥AB交射线BC于点E,以DE为直径作圆,另一个动点G以相同速度从A出发向B运动,作GH⊥AB交射线AC于点H,当GH与⊙F相切时,求出DE的值.
分析 作FQ⊥QG于Q,如图,根据切线的性质得FQ=$\frac{1}{2}$DE,再证明四边形FQGD为正方形得到DG=FG=$\frac{1}{2}$DE,再利用勾股定理计算出AB=10,接着证明Rt△BDE∽Rt△BCA,利用相似比可得BD=$\frac{4}{3}$DE,然后利用BD=AG得到$\frac{4}{3}$DE+$\frac{1}{2}$DE+$\frac{4}{3}$DE=10,然后就解方程即可.
解答 解:作FQ⊥QG于Q,如图,
∵GH与⊙F相切,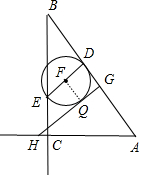
∴FQ=$\frac{1}{2}$DE,
∵DE⊥AB,HG⊥AB,
∴四边形FQGD为正方形,
∴DG=FG=$\frac{1}{2}$DE,
在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠EBD=∠ABC,
∴Rt△BDE∽Rt△BCA,
∴DE:AC=BD:BC,即DE:6=BD:8,
∴BD=$\frac{4}{3}$DE,
∵BD=AG,
∴$\frac{4}{3}$DE+$\frac{1}{2}$DE+$\frac{4}{3}$DE=10,
∴DE=$\frac{60}{19}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
18.已知α为锐角,若tanα=$\frac{1}{2}$,则cosα等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
16.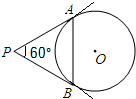 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
3.关于x的方程x2+(m-2)x+m+1=0有两个相等的实数根,则m的值是( )
| A. | 0 | B. | 8 | C. | 4$±\sqrt{2}$ | D. | 0或8 |
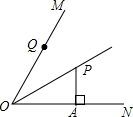 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=1,则PQ的最小值为1.
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=1,则PQ的最小值为1.